

| НАЧАЛО |
| ПРОГНОЗ |
| СТАТЬИ |
|
4.Загадка цунами: земных и космических
|
| ССЫЛКИ |
| КОНТАКТЫ |
ЗАГАДКА ЦУНАМИ: ЗЕМНЫХ И КОСМИЧЕСКИХ
 |
В житейском море зыбь морская Меня то крутит, то бросает. Вздымаясь, падают валы На плечи грешной головы. Подхвачен вихрем утлый челн - То вверх, то вниз По воле волн. Миг ... и любви «девятый вал» Вдруг неожиданно поднял Над бездною ревущих волн, Понес вперед... Надеждой полн, Взывая к звездам, Им кричу, Раскинув руки, И... лечу... В.И. Козлов. |
 |
Валерий Игнатьевич Козлов, доктор физико-математических наук, главный научный сотрудник лаборатории теории космической плазмы Института космофизических исследований и аэрономии им. Ю.Г. Шафера СО РАН. |
КРАХ ПАРАДИГМЫ «ЛИНЕЙНОГО МИРА»
Казалось бы, что может быть общего между печально известной волной цунами, загадочной одиночной «волной-убийцей» в океане, известной также как «девятый вал», с одной стороны, и гелиосферной бурей и... 11-летним циклом, с другой? По мнению автора, объединяет их общность происхождения. Природа тех и других связана с проявлением нелинейности явлений, которая не является досадным исключением из линейного, как представлялось, характера законов природы.Наиболее сложным периодом в науке является этап смены научной парадигмы - господствующих в данное время научных представлений о мире или характере физических законов. Раскрытие загадки волн цунами и одиночной океанской «волны-монстра» неожиданно для многих оказалось связанным как раз со сменой парадигмы «линейности», или «принципа суперпозиции», в науке.
Во всех линейных моделях скорость распространения волны в воде определяется характеристикой среды - глубиной водоема и постоянной ускорения свободного падания. Но глубина водоема обычно различна, и значит, скорость волны (которая пропорциональна локальной глубине водоема) выше на гребне и ниже во впадине. Поэтому гребень опережает впадину - происходит укручение профиля волны и ее последующее опрокидывание.
С другой стороны, известно, что скорость распространения волны зависит от ее длины - явление дисперсии. Высшие гармоники, которые возникают при нелинейном искажении профиля волны, за счет дисперсии будут либо обгонять основную волну, либо отставать от нее в зависимости от того, растет или убывает групповая скорость с увеличением волнового числа (величина, обратная длине волны). Вследствие дисперсии исходная волна «расползается» на отдельные волновые пакеты еще до ее опрокидывания. В случае же компенсации нелинейного укручения дисперсионным расплыванием возможна реализация стационарной бегущей волны, то есть волны, профиль которой не изменяется со временем. Такая волна и называется солитоном (от английского «solitary wave» -одиночная волна).
ОТКРЫТИЕ ЭКЗОТИЧЕСКОЙ ВОЛНЫ - СОЛИТОНА
Первым наблюдал и описал солитон шотландский инженер викторианской эпохи Джон Скотт Рассел. В 1834 г. он занимался изучением волн, вызванных движением по каналу баржи. В одном из экспериментов баржа неожиданно остановилась, а масса воды, которую она привела в движение, собралась у носа судна и ... оторвавшись от него, покатилась по каналу с большой скоростью в виде уединенного возвышения, не меняющего своей формы и не снижающего скорости. На протяжении всей жизни Рассел неоднократно возвращался к результатам этого эксперимента, поскольку верил, что открытая им уединенная волна должна выражать общую закономерность многих процессов в природе. К сожалению, работа Рассела, опубликованная лишь через 10 лет (1844 г.), вызвала неоднозначную реакцию в научной среде. На континенте она осталась незамеченной, а в Англии подверглась жесточайшей критике. Более того, именитые современники Рассела сомневались в самом факте существования подобных волн [1].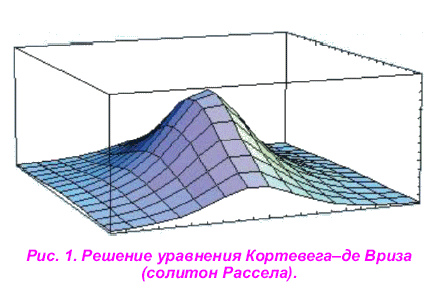 Лишь через 30 лет Буссинеск и Рэлей независимо друг от друга нашли аналитическую формулу для «волны возвышения» и вычислили скорость ее распространения,
которая зависела от амплитуды. Еще через 60 лет Кортевег и де Вриз, используя уравнения гидродинамики, получили нелинейное уравнение для волн, амплитуда которых много меньше, а длина много больше глубины бассейна:
ut+6*u*ux+uxxx=0, где индексы
t и х при скорости u означают соответствующие производные. Оказалось, что решение этого уравнения имеет вид гиперболического секанса (рис. 1) и является уединенной волной, которую Рассел наблюдал еще в 1834 г.
Лишь через 30 лет Буссинеск и Рэлей независимо друг от друга нашли аналитическую формулу для «волны возвышения» и вычислили скорость ее распространения,
которая зависела от амплитуды. Еще через 60 лет Кортевег и де Вриз, используя уравнения гидродинамики, получили нелинейное уравнение для волн, амплитуда которых много меньше, а длина много больше глубины бассейна:
ut+6*u*ux+uxxx=0, где индексы
t и х при скорости u означают соответствующие производные. Оказалось, что решение этого уравнения имеет вид гиперболического секанса (рис. 1) и является уединенной волной, которую Рассел наблюдал еще в 1834 г.
Драматизм ситуации, связанной с открытием Расселом уединенной волны, можно представить по высказыванию профессора Н.А. Кудряшова: «В настоящее время кажется странным, что открытие Рассела и его последующее подтверждение в работе Кортевега и де Вриза не получили заметного резонанса в науке. Эти работы оказались забытыми почти на 70 лет. Один из авторов уравнения, Д.Д. Кортевег, прожил долгую жизнь и был известным ученым. Но когда в 1945 году научная общественность отмечала его 100-летний юбилей, то в списке лучших публикаций работа, выполненная им совместно с де Вризом, даже не значилась. Составители списка сочли эту работу Кортевега не заслуживающей внимания. И только спустя еще четверть века именно эта работа стала считаться главным научным достижением Кортевега.
Однако если поразмыслить, то такое невнимание к уединенной волне Рассела становится понятным. Дело в том, что в силу своей специфичности это открытие долгое время считалось довольно частным фактом. В самом деле, в то время физический мир казался линейным, и принцип суперпозиции считался одним из фундаментальных принципов большинства физических теорий. Поэтому никто из исследователей не придал открытию экзотической волны на воде серьезного значения» [1, стр. 86].
АНАЛОГИЯ С НЕЛИНЕЙНЫМ ОСЦИЛЛЯТОРОМ
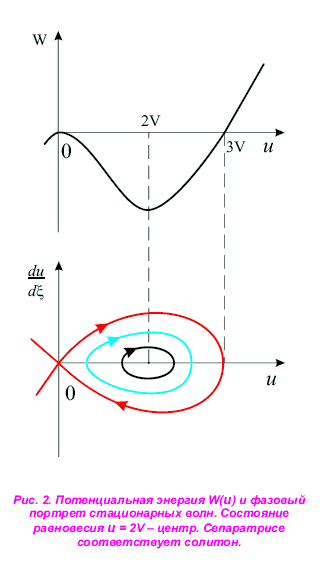 Уравнение Кортевега-де Вриза можно привести к виду известного уравнения для нелинейного осциллятора - материальной точки с условной массой
β, движущейся в потенциальной яме
W(u)(рис. 2), причем новая (бегущая) координата, или переменная
ζ = x-V*t, играет роль времени (V- скорость волн). Существуют различные классы решений этого уравнения:
Уравнение Кортевега-де Вриза можно привести к виду известного уравнения для нелинейного осциллятора - материальной точки с условной массой
β, движущейся в потенциальной яме
W(u)(рис. 2), причем новая (бегущая) координата, или переменная
ζ = x-V*t, играет роль времени (V- скорость волн). Существуют различные классы решений этого уравнения:
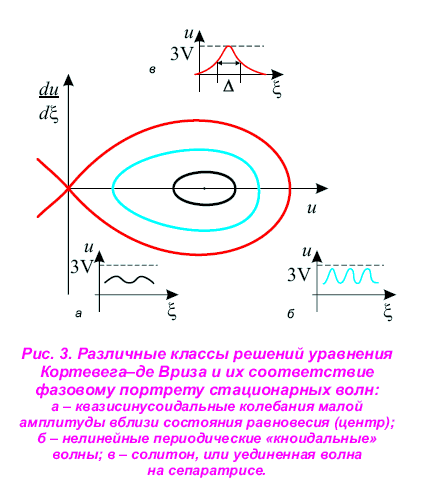
1) квазисинусоидальные колебания с малыми амплитудами (фазовые траектории вблизи состояния равновесия - центр), для них нелинейность почти не сказывается (рис. 3, а);
2) нелинейные периодические движения вблизи сепаратрисы , называемые «кноидальными» волнами (рис. 3,6);
3) самой сепаратрисной петле соответствует локализованное в пространстве решение в виде одиночного возвышения, или уединенной волны - солито-на, с максимальной скоростью или амплитудой ЗУ (рис.3, в). Солитон имеет бесконечные «хвосты» по краям, поскольку время достижения волной состояния равновесия вблизи «седла» (в начале координат) очень велико. В такое состояние система входит с предельно малой скоростью, то есть бесконечно долго. На языке осцилляторной модели сказанное означает, что на графике потенциальной энергии точка массы β длительное время находится в положении u = 0 (начало координат на рис. 2, 3). Затем она скатывается в потенциальную яму W(u), достигает максимального значения скорости u = 3*V, где W(u) во второй раз обращается в нуль, отражается от высокого края потенциальной ямы и столь же медленно возвращается снова в положение u = 0 [2].
ВСЕ ДОРОГИ ВЕДУТ К... СОЛИТОНУ
Для уравнения Кортевега-де Вриза имеет место инвариант umax*Δ2 = const, т.е. произведение величины максимальной скорости (или амплитуды) солитона на квадрат его ширины (Δ) есть величина постоянная. Из этого следует, что чем выше солитон, тем он уже! Запомним это. При нормировке (делении) на правую часть этого инварианта удобно ввести безразмерную величину σ, которая пропорциональна максимальной величине скорости umax. Поэтому величину σ можно условно принять за параметр нелинейности волны. Для σ << 1 возмущение имеет очень малую амплитуду скорости, и его можно считать линейным. При σ = 1 нелинейность из-за увеличения амплитуды уравновешивается дисперсией - солитон.Наибольший интерес представляет случай σ >> 1. На первой стадии эволюции такого возмущения дисперсия не играет роли, так как его поведение определяется нелинейностью: доминирует тенденция к укручению профиля и последующему его опрокидыванию. Однако при появлении более высоких гармоник в игру вступает дисперсия, которая будет «разводить» возмущения с различными длинами волн. Поэтому по прошествии достаточно большого промежутка времени возмущение должно «рассыпаться» - разбиться на отдельные группы, аналогичные волновым пакетам в линейном случае, движущимся почти с постоянной скоростью. Но все решения,
 отвечающие бегущим волнам с постоянной скоростью, известны: это периодические (линейные) волны с σ < 1 и солитоны с σ
= 1 . Никаких других решений нет! Следовательно, начальный импульс с σ
>> 1 должен «рассыпаться» на солитоны и слабо нелинейный пакет. Поэтому в конце концов останутся
практически только солитоны! [3]. Почему солитоны, то есть частные виды стационарных волн, так интересны? Фактически, по той же причине, что и другие стационарные волны: «...
нестационарные возмущения довольно широкого класса в процессе распространения асимптотически приближаются к
солитону!» [4, стр. 308].
отвечающие бегущим волнам с постоянной скоростью, известны: это периодические (линейные) волны с σ < 1 и солитоны с σ
= 1 . Никаких других решений нет! Следовательно, начальный импульс с σ
>> 1 должен «рассыпаться» на солитоны и слабо нелинейный пакет. Поэтому в конце концов останутся
практически только солитоны! [3]. Почему солитоны, то есть частные виды стационарных волн, так интересны? Фактически, по той же причине, что и другие стационарные волны: «...
нестационарные возмущения довольно широкого класса в процессе распространения асимптотически приближаются к
солитону!» [4, стр. 308].
НЕОЖИДАННОЕ ПРОДОЛЖЕНИЕЕ
Драматическая история открытия Расселом уединенной волны получила не менее драматическое продолжение. Имеются в виду известные события, относящиеся к парадоксу Ферми-Паста-Улама (ФПУ). В 1952 г. по просьбе знаменитого итальянского физика-теоретика Энрико Ферми изучалась (на ЭВМ) проблема термализации (перераспределения) энергии по модам (гармоникам колебаний) в системе осцилляторов, связанных нелинейными пружинами. Ожидалось, что при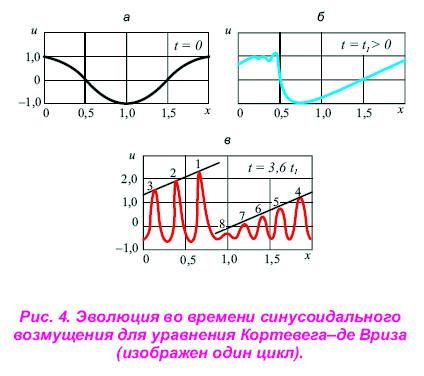 учете в возвращающей силе квадратичной нелинейной добавки, моды колебаний не будут независимыми, то есть начнется их нелинейное взаимодействие - медленная (по сравнению с периодом мод) перекачка энергии от
моды к моде. Ферми, Паста и Улам предполагали, что энергия в конце концов равномерно распределится между модами - произойдет термализация энергии по степеням свободы в полном соответствии со вторым началом термодинамики. Но результат оказался удивительным.
Вместо термализации наблюдался длительно повторяющийся процесс перекачки энергии от самой низкой моды к низким и
обратно! (рис. 4, а, б, в). Парадокс ФПУ был разрешен лишь в 1965 г., когда Мартин Крускал и Норманн Забусски установили
эквивалентность (в пределе) дискретной системы уравнений связанных осцилляторов Ферми- Паста-Улама и уравнения Кортевега-де Вриза. Вот тут-то Забусски и Крускал обнаружили нечто удивительное, о чем, впрочем, знал Рассел: при взаимодействии два почти одинаковых импульса, казалось, обменивались своими свойствами. Действительно,
передний меньший импульс становился выше и уже, когда к нему подходил передний фронт большего импульса.
Больший импульс, в свою очередь, приобретал свойства меньшего (в этом смысле, импульсы больше похожи на частицы). Когда же амплитуды импульсов сильно различались, больший импульс «проходил» сквозь меньший).
учете в возвращающей силе квадратичной нелинейной добавки, моды колебаний не будут независимыми, то есть начнется их нелинейное взаимодействие - медленная (по сравнению с периодом мод) перекачка энергии от
моды к моде. Ферми, Паста и Улам предполагали, что энергия в конце концов равномерно распределится между модами - произойдет термализация энергии по степеням свободы в полном соответствии со вторым началом термодинамики. Но результат оказался удивительным.
Вместо термализации наблюдался длительно повторяющийся процесс перекачки энергии от самой низкой моды к низким и
обратно! (рис. 4, а, б, в). Парадокс ФПУ был разрешен лишь в 1965 г., когда Мартин Крускал и Норманн Забусски установили
эквивалентность (в пределе) дискретной системы уравнений связанных осцилляторов Ферми- Паста-Улама и уравнения Кортевега-де Вриза. Вот тут-то Забусски и Крускал обнаружили нечто удивительное, о чем, впрочем, знал Рассел: при взаимодействии два почти одинаковых импульса, казалось, обменивались своими свойствами. Действительно,
передний меньший импульс становился выше и уже, когда к нему подходил передний фронт большего импульса.
Больший импульс, в свою очередь, приобретал свойства меньшего (в этом смысле, импульсы больше похожи на частицы). Когда же амплитуды импульсов сильно различались, больший импульс «проходил» сквозь меньший).
ТАЙНА «ДЕВЯТОГО ВАЛА» РАСКРЫТА!?
 До 60-х годов прошлого века считалось, что нелинейные уравнения могут иметь только частные решения, удовлетворяющие специально заданным начальным условиям. Однако уравнение Кортевега-де Вриза и в этом случае оказалось в исключительном положении [1]. Это подтверждается историей, связанной с загадкой происхождения таинственного «девятого вала». С незапамятных времен люди наблюдали группы волн на воде. И лишь в 1967 г. было установлено, что простая периодическая волна на глубокой воде
неустойчива и разбивается на группы (неустойчивость Бенжамена-Фейера). Уравнение, описывающее распространение групп волн на воде было получено В.Е. Захаровым в 1968 г. Причем, полученное уравнение было уже известно физикам (нелинейное уравнение Шредингера). Однако самое удивительное в том, что оно имеет
решение в виде солитонов! Правда, солитоны уравнения Шредингера отличаются от солитонов Кортевега-де Вриза тем, что они соответствуют форме
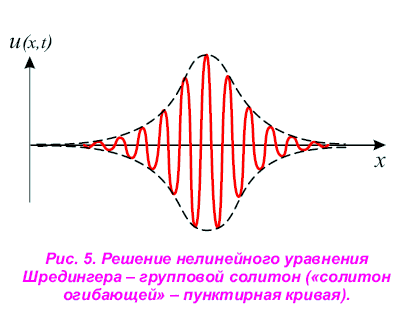
огибающей группы волн. Это - так называемый групповой солитон, или «солитон огибающей» (рис. 5). Он движется со скоростью, отличной от скорости движения самих волн, причем они почти
монохроматичны! И - внимание! - «...под огибающей может спрятаться от 14 до 20 волн, причем средняя - самая высокая. В этом -объяснение "девятого вала": самая высокая в группе -седьмая-десятая волна» [2, стр. 94].
До 60-х годов прошлого века считалось, что нелинейные уравнения могут иметь только частные решения, удовлетворяющие специально заданным начальным условиям. Однако уравнение Кортевега-де Вриза и в этом случае оказалось в исключительном положении [1]. Это подтверждается историей, связанной с загадкой происхождения таинственного «девятого вала». С незапамятных времен люди наблюдали группы волн на воде. И лишь в 1967 г. было установлено, что простая периодическая волна на глубокой воде
неустойчива и разбивается на группы (неустойчивость Бенжамена-Фейера). Уравнение, описывающее распространение групп волн на воде было получено В.Е. Захаровым в 1968 г. Причем, полученное уравнение было уже известно физикам (нелинейное уравнение Шредингера). Однако самое удивительное в том, что оно имеет
решение в виде солитонов! Правда, солитоны уравнения Шредингера отличаются от солитонов Кортевега-де Вриза тем, что они соответствуют форме
огибающей группы волн. Это - так называемый групповой солитон, или «солитон огибающей» (рис. 5). Он движется со скоростью, отличной от скорости движения самих волн, причем они почти
монохроматичны! И - внимание! - «...под огибающей может спрятаться от 14 до 20 волн, причем средняя - самая высокая. В этом -объяснение "девятого вала": самая высокая в группе -седьмая-десятая волна» [2, стр. 94].
СОЛИТОННАЯ ПРИРОДА ГЕЛИОСФЕРНОЙ БУРИ И ... 11-ЛЕТНЕГО ЦИКЛАА
В предыдущих публикациях автора данной статьи говорилось о введении им в начале восьмидесятых годов нового индекса солнечной активности - индекса мерцаний космических лучей [5-7]. По сути, он является показателем частотного спектра флуктуации. Показатель спектра, в свою очередь, определяется, как величина наклона линейного тренда огибающей всех амплитуд гармоник частотного спектра.Известно, что амплитуды всех гармоник идеального случайного сигнала, или «белого шума», в среднем равны. Следовательно, наклон линейного тренда огибающей гармоник спектра идеального случайного сигнала, то есть показатель спектра для «белого шума», равен нулю. Именно такой вид в среднем имеет частотный спектр флуктуации интенсивности галактических космических лучей (ГКЛ) в изучаемом нами диапазоне периодов их флуктуации (100-10000 с).
Значимые и систематические изменения показателя частотного спектра флуктуации космических лучей в возмущенный период мы связываем с модуляцией фонового шумоподобного спектра флуктуации ГКЛ вариациями межпланетного магнитного поля во время усиления активности Солнца.
Если в традиционной радиотехнике «несущей» является фиксированная радиочастота, подверженная модуляции акустическим сигналом на входе радиопередатчика и демодуляции звукового сигнала на выходе радиоприемника, то в нашем случае мы имеем дело, образно говоря, с «хаотической несущей»! Следовательно, необходимо было решить проблему демодуляции, с целью выявления полезного сигнала от солнечного источника. В этом смысле можно сказать, что своеобразный «пульс Солнца» давно уже передается нам через модуляцию шумоподобного фона космического излучения. Оставалось только его услышать.
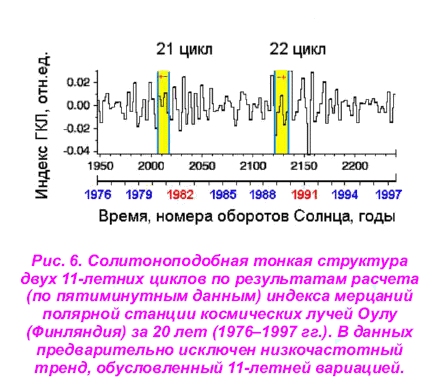 В итоге нами была обнаружена тонкая структура 11-летнего цикла - нестационарный переходный колебательный процесс смены знака общего магнитного поля Солнца (рис. 6). При этом установлена обратная зависимость длительности переходного колебательного процесса от его амплитуды. Это означает неизменность площади под кривой единичного 11-летнего цикла, то есть наличие инварианта: «амплитуда-длительность» [8-9]. В таком случае уменьшение амплитуды неизбежно влечет за собой увеличение продолжительности солнечного цикла и наоборот.
В итоге нами была обнаружена тонкая структура 11-летнего цикла - нестационарный переходный колебательный процесс смены знака общего магнитного поля Солнца (рис. 6). При этом установлена обратная зависимость длительности переходного колебательного процесса от его амплитуды. Это означает неизменность площади под кривой единичного 11-летнего цикла, то есть наличие инварианта: «амплитуда-длительность» [8-9]. В таком случае уменьшение амплитуды неизбежно влечет за собой увеличение продолжительности солнечного цикла и наоборот.
Нечто похожее было установлено ранее и другими авторами. На существование обратной зависимости между временем достижения максимумов 11-летнего цикла и его амплитуды указывалось ранее Вальдмайером [10]. Обратная зависимость между временем достижения максимума цикла и квадратным корнем из амплитуды цикла выявлена и в недавней работе Э.В. Кононовича[11].
Похожая зависимость характерна для «солитона огибающей» (ширина солитона обратно пропорциональна корню квадратному из его амплитуды). Все это указывает на солито-ноподобную природу 11-летнего цикла, обладающую самоподобными, т.е. скейлинговыми или фрактальными свойствами [12-13].
Действительно, на меньших масштабах самоподобные или фрактальные свойства обнаруженных осцилляции проявляются в солитоноподобной природе гелио-сферного токового слоя в период гелиосферной бури (рис. 7) [14-15]. Как и для солитона, момент регистрации максимальной амплитуды вариаций индекса мерцаний приходится на минимальный период вариаций. На это указывает характерный вейвлет-образ гелиосферной бури в космических лучах: в виде своеобразной «летающей тарелки». Это хорошо видно при сопоставлении амплитуды огибающей вариаций индекса (в нижней части рисунка) со структурой того же вейвлет-образа: максимум амплитуды огибающей приходится на наименьший период вариаций, который совпадает с серединой «летающей тарелки».
Эпилог
Формирование солитоноподобной структуры в гелиосферном токовом слое является важным с различных точек зрения. Прежде всего, это означает, что нет взаимнооднозначного соответствия между спорадическими (отдельно взятыми) событиями на Солнце и их проявлениями на орбите Земли: гелиосферный токовый слой обладает собственной «передаточной функцией», до неузнаваемости искажающий такой солнечный «сигнал». Таким образом, область между Солнцем и Землей давно уже не является межпланетным пространством, а есть межпланетная среда, точнее - солнечная корона, проявляющая удивительные свойства в периоды экстремальной солнечной активности! Что касается возможной солитонной природы 11-летнего цикла, то это может означать, что сама 11-летняя цикличность есть эффективный (солитонный) механизм регуляции энергии Солнца, предотвращающий от «перегрева» при критической температуре. Основные положения данной статьи были доложены ее автором на международном симпозиуме по современным наблюдениям и моделированию в системе «Солнце-Земля». На конференции не обошлось и без интригующих моментов: доклад о солитонной природе 11-летнего цикла [9] был поставлен оргкомитетом симпозиума, вряд ли случайно, перед докладом финских коллег с похожим (по сути) названием: «Гелиосферное магнитное поле: застенчивая балерина, танцующая в темпе вальса» [16]. Как видно, «горячие» финские парни были настолько поражены красотой обнаруженного ими эффекта, что не удержались от возвышенного слога. Нам же удалось не только увидеть удивительную гармонию, но и разгадать природу (солитонную, как мне представляется) явления, наблюдаемого в верхней короне Солнца.Литература
1. Кудряшов Н.А. Нелинейные волны и солитоны// Соросовский образовательный журнал. - 1997. -№2.-С. 85-91.2. Трубецков Д.И. Введение в синергетику. Хаос и структуры. - М.: Едиториал УРСС, 2004. - 235 с.
3. Кадомцев Б.Б. Коллективные явления в плазме. -М.: Наука, 1988.- 304 с.
4. Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. - М.: Наука, 1984.-432 с.
5. Козлов В.И. Космическая Погода. Мифы и реальность // Наука и техника в Якутии. - 2002. -№1(2).-С. 17-20.
6. Козлов В.И. Горизонты предсказуемости. Очевидное - невероятное // Наука и техника в Якутии. -2003.-№2(5).-С. 11-14.
7. Козлов В.И. Грядет ли сбой 11-летнего солнечного цикла?//Наука и техника в Якутии. - 2006. -№1(10).-С. 51-56.
8. Козлов В.И., Марков В.В. Вейвлет-образ тонкой структуры 11-летнего цикла по исследованию флуктуации космических лучей в 20-23 циклах // Геомагнетизм и аэрономия. - 2007. -№1.
9. Kozlov V.I., Markov V.V. Soliton-similarnature of 11-year solar activity cycle // Abstracts of International Symposium «Recent Observations and Simulations of the Sun-Earth System». - Varna, Bulgaria, September 17-22. -2006. -C. 63.
10. Витинский Ю.И. Копецкий М., Куклин Г.В. Статистика пятнообразовательной деятельности Солнца. - Москва: Наука, 1986. -201с.
11. Кононович Э.В. Аналитические представления средних вариаций солнечной активности в течение цикла // Геомагнетизм и аэрономия. - 2005. - 1.45.-№3.-С. 316-323.
12. Козлов В.И. Масштабная инвариантность динамики флуктуации космических лучей на геоэффективных фазах солнечного цикла//Геомагнетизм и аэрономия. - 1999. - Т. 39. -№1.- С. 96-99.
13. Козлов В.И. Оценка скейлинговых свойств динамики флуктуации космических лучей в цикле солнечной активности//Геомагнетизм и аэрономия. -1999.-Т.39.-№1.-С. 100-104.
14. Козлов В.И., Марков В.В. Вейвлет-образ гелиосферной бури в космических лучах // Геомагнетизм и аэрономия. -2007. -№1.
15. Kozlov V.I., Markov V.V. Soliton-similar Image of Heliospheric Storm //Abstracts of International Symposium «Recent Observations and Simulations of the Sun-Earth System,. - Varna, Bulgaria, September 17-22. - 2006. -C.63.
16. Mursula K. Heliospheric Magnetic Field: the Bashful Balerina Dancing in Waltz Tempo//Abstracts of International Symposium «Recent Observations and Simulations of the Sun-Earth System». - Varna, Bulgaria, September 17-22. -2006.-C. 78- http://www.isroses.org