

| НАЧАЛО |
| ПРОГНОЗ |
| СТАТЬИ |
|
2.Грядет ли сбой 11-летнего солнечного цикла?
|
| ССЫЛКИ |
| КОНТАКТЫ |
ГРЯДЕТ ЛИ СБОЙ 11-ЛЕТНЕГО СОЛНЕЧНОГО ЦИКЛА?
 |
Улыбка Моны Лизы Таилась на губах. Какая Мона Лиза? Увы и Ах! Но что за наважденье, Что на меня нашло? Конечно, показалось, Мелькнуло и... прошло. И снова Леонардо В ее глазах! Так, может, Леонардо Живет в веках? Я глаз поднять не смею, Боясь спугнуть его - Прекрасное видение - Улыбку Леонардо, Сквозь образ Моны Лизы Видение мое. В. Козлов, 1996. |
 |
Валерий Игнатьевич Козлов, доктор физико-математических наук, главный научный сотрудник лаборатории теории космической плазмы Института космофизических исследований и аэрономии им. Ю.Г. Шафера СО РАН. |
ВОПРОСЫ БЕЗ ОТВЕТОВ
Максимум и минимум солнечной активности, 11-летний цикл, солнечные пятна, магнитные бури - вот далеко не полный список узнаваемых терминов, появляющихся в печати, на радио и телевидении с завидным постоянством примерно через каждые 11 лет. Светимость Солнца (или полный поток солнечного излучения в видимом и инфракрасном диапазоне, подпитываемый термоядерным источником в центре) практически неизменна. В связи с этим ее часто так и называют - солнечная постоянная. В чем секрет удивительного постоянства светимости Солнца, какова природа цикличности солнечной активности и, что не менее важно, какова причина ее длительных сбоев? Однозначного ответа на эти вопросы до сих пор нет. Объясняют 11-летний цикл, исходя из точки зрения, что он является свойством динамо-процессов. Механизм его неясен, но представляется, что он действует независимо от динамо, модулируя активность последнего [1]. Ниже предлагается гипотеза автора о природе цикличности Солнца, которая в состоянии дать ответ на поставленные выше вопросы с единой позиции.НОВЫЙ ИНДЕКС СОЛНЕЧНОЙ АКТИВНОСТИ
Принято считать, что 11-летняя цикличность Солнца была установлена в середине XIX в. известным немецким ученым Р. Вольфом по данным систематических
наблюдений за солнечными пятнами, открытыми Галилео Галилеем после изобретения им телескопа. С тех пор так
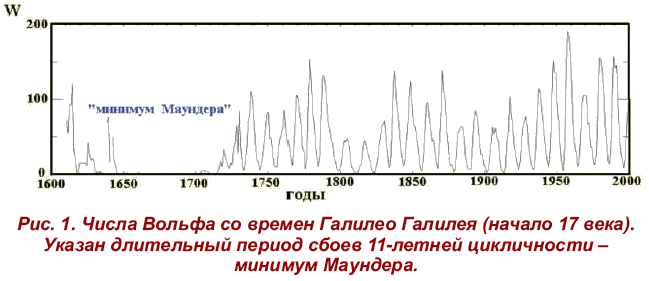 называемые числа Вольфа W (суммарное число
пятен на видимой части солнечного диска) и служат характеристикой активности Солнца, хотя и не единственной (рис. 1).
В наше время были предложены и другие, более физические характеристики. Такие, например, как поток радиоизлучения на фиксированной
длине волны. После открытия космических лучей была установлена взаимосвязь чисел Вольфа в 11-летнем цикле с интенсивностью галактических космических лучей (ГКЛ). По сравнению с субъективностью оценок чисел Вольфа, поток солнечного радиоизлучения и поток космических лучей являются более объективными, хотя и опосредованными характеристиками активности Солнца.
Подобно тому, как все живое в процессе эволюции «научилось» видеть земные объекты в обычном свете (словно зная, что движения со скоростью, большей скорости света быть не может), мы тоже научились «видеть» взрывные ударные волны от
называемые числа Вольфа W (суммарное число
пятен на видимой части солнечного диска) и служат характеристикой активности Солнца, хотя и не единственной (рис. 1).
В наше время были предложены и другие, более физические характеристики. Такие, например, как поток радиоизлучения на фиксированной
длине волны. После открытия космических лучей была установлена взаимосвязь чисел Вольфа в 11-летнем цикле с интенсивностью галактических космических лучей (ГКЛ). По сравнению с субъективностью оценок чисел Вольфа, поток солнечного радиоизлучения и поток космических лучей являются более объективными, хотя и опосредованными характеристиками активности Солнца.
Подобно тому, как все живое в процессе эволюции «научилось» видеть земные объекты в обычном свете (словно зная, что движения со скоростью, большей скорости света быть не может), мы тоже научились «видеть» взрывные ударные волны от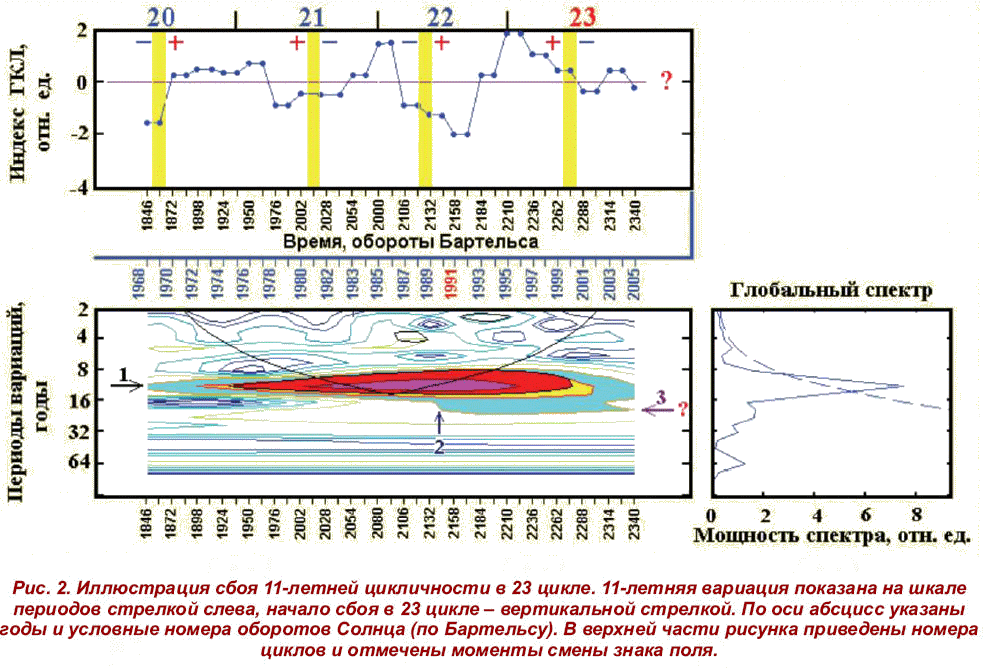 солнечных вспышек в «свете» космических лучей, движущихся, кстати, также с околосветовой скоростью. В этой, возможно, единственной ситуации термин «лучи» (космические) оправдывает свое название. В действительности космические лучи - это частицы. Протоны, например, из которых преимущественно эти лучи и состоят. Но в отличие от фотонов (квантов света) они обладают массой и зарядом.
Очевидно, что космические лучи, как и все заряженные частицы, подвержены воздействию магнитного поля, в данном случае межпланетного.
Искажения магнитного поля, вызванные взрывами на Солнце, практически мгновенно сказываются на космических лучах. В этом смысле можно сказать, что своеобразный «пульс Солнца» давно уже передается нам через модуляцию шумоподобного фона космического излучения. Оставалось только его услышать!
В начале восьмидесятых годов автором был введен индекс мерцаний (усиленных флуктуации) интенсивности ГКЛ [2-3]. Использование нового индекса позволило получить и новые результаты. Если говорить кратко, то они заключаются в обнаружении гигантской волны переполюсовки общего магнитного поля Солнца. Точнее, речь идет об обнаружении нестационарного переходного колебательного процесса смены знака общего поля Солнца, длительностью т = 3 + 1 год [4]. Причем продолжительность такого переходного процесса
обратно пропорциональна амплитуде 11-летнего цикла.
солнечных вспышек в «свете» космических лучей, движущихся, кстати, также с околосветовой скоростью. В этой, возможно, единственной ситуации термин «лучи» (космические) оправдывает свое название. В действительности космические лучи - это частицы. Протоны, например, из которых преимущественно эти лучи и состоят. Но в отличие от фотонов (квантов света) они обладают массой и зарядом.
Очевидно, что космические лучи, как и все заряженные частицы, подвержены воздействию магнитного поля, в данном случае межпланетного.
Искажения магнитного поля, вызванные взрывами на Солнце, практически мгновенно сказываются на космических лучах. В этом смысле можно сказать, что своеобразный «пульс Солнца» давно уже передается нам через модуляцию шумоподобного фона космического излучения. Оставалось только его услышать!
В начале восьмидесятых годов автором был введен индекс мерцаний (усиленных флуктуации) интенсивности ГКЛ [2-3]. Использование нового индекса позволило получить и новые результаты. Если говорить кратко, то они заключаются в обнаружении гигантской волны переполюсовки общего магнитного поля Солнца. Точнее, речь идет об обнаружении нестационарного переходного колебательного процесса смены знака общего поля Солнца, длительностью т = 3 + 1 год [4]. Причем продолжительность такого переходного процесса
обратно пропорциональна амплитуде 11-летнего цикла.
В ОЖИДАНИИ ИСЧЕЗНОВЕНИЯ ЦИКЛИЧНОСТИ СОЛНЦА
Выявленная нами обратная зависимость длительности переходного процесса от амплитуды 11-летнего цикла указывает на наличие инварианта «длительность - амплитуда». Нечто похожее было установлено ранее и другими авторами. На существование обратной зависимости между временем достижения максимумов 11-летнего цикла и его амплитуды указывалось ранее Вальдмайером [5]. Обратная зависимость между временем достижения максимума цикла и квадратным корнем из максимальной амплитуды цикла выявлена и в недавней работе Э.В. Коно-новича [6]. Все вышеотмеченное указывает на наличие инварианта или, другими словами, на неизменность площади под кривой единичного 11-летнего цикла. Это означает, что уменьшение амплитуды неизбежно влечет за собой увеличение продолжительности цикла и наоборот. Временной ход 11-летней вариации в индексе мерцаний ГКЛ показан в верхней части рис. 2. Для каждого 11-летнего цикла (с условно принятыми номерами 20-23) отмечены моменты смены знака общего магнитного поля Солнца. В исходных данных предварительно исключен низкочастотный тренд. В течение трех циклов 20-22 в индексе мерцаний ГКЛ доминирует отчетливо выраженная 11-летняя гармоника. Ее местоположение на шкале периодов вариаций показано горизонтальной стрелкой слева (№1). Начиная с 23 цикла, точнее, с конца предыдущего 22 цикла (ориентировочно с 1991 г.) происходит разрушение 11-летней цикличности. Момент начала ее сбоя показан вертикальной стрелкой (№ 2). Сбой проявляется в дрейфе максимума 11-летней гармоники в область больших периодов вариаций, то есть в низкочастотную область. Она отмечена горизонтальной стрелкой справа (№ 3). Только при наличии инварианта «амплитуда - длительность» уменьшение амплитуды 23 цикла будет сопровождаться увеличением его продолжительности, а в пределе - нарушением 11-летней цикличности. Один из длительных сбоев солнечной цикличности носит название «минимум Маундера» (см. рис. 1). И именно перед минимумом Маундера было зарегистрировано увеличение периода солнечного цикла [1]. Имеются еще два аргумента в пользу вывода о начавшемся сбое 11-летней цикличности. Во-первых, существует известное правило Гневышева - Оля, согласно которому амплитуда нечетного цикла больше амплитуды предыдущего четного. Не оправдавшиеся прогнозы о большой амплитуде текущего 23 цикла были основаны на использовании именно этого правила. И нарушено оно именно в 23 цикле [7], а по нашим данным еще раньше - в конце предыдущего 22 цикла (см. рис. 2). Такое случается нечасто, и только перед длительными сбоями 11-летнего цикла. Нарушение цикличности Солнца означает снижение его активности. О том, что такое возможно, указывает независимо и ожидаемый минимум вековой (-100 летней) вариации солнечной активности, достоверность которой (в числах Вольфа) подтверждается современными методами вейвлет-анализа [1]. В отличие от традиционного спектрально-временного представления, вейвлет-анализ (вейвлет, дословно - маленькая волна) позволяет наиболее точно передать амплитудно-частотную динамику процесса во времени.11-ЛЕТНИЙ ЦИКЛ - МЕХАНИЗМ РЕГУЛЯЦИИ ТЕМПЕРАТУРЫ
Постоянство площади, заключенной под кривой единичного 11-летнего цикла, означает неизменность величины энергии, «стравливаемой» в единичном цикле. Это указывает, в свою очередь, на возможную природу цикличности Солнца: 11-летняя в среднем цикличность -автоколебательный механизм регуляции температуры, предотвращающий Солнце от «перегрева». Автоколебательной называют динамическую систему, преобразующую энергию источника в энергию незатухающих колебаний, характеристики которых определяются в основном параметрами самой системы. В качестве возможной модели 11-летнего цикла, в рамках которой можно объяснить как возникновение, так и исчезновение 11-летней цикличности, предлагается модель термогравитационной конвекции Рэлея-Бенара. Подобная модель, описываемая системой уравнений Навье-Стокса и теплопроводности, сводится к известной системе Лоренца с тремя независимыми переменными [8]: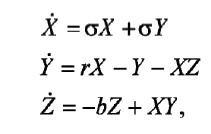 где переменная X пропорциональна скорости циркуляции жидкости; У характеризует разность температур между восходящими и нисходящими потоками жидкости; переменная
Z пропорциональна отклонению вертикального профиля температуры от равновесного значения;
b - безразмерный параметр, определяющий геометрию системы; число Прандтля
σ-физический параметр жидкости, показывающий отношение коэффициентов кинематической вязкости и температуропроводности;
r -управляющий параметр, пропорциональный разности температур, или число Рэлея, нормированное на свое критическое значение.
Система Лоренца в состоянии
где переменная X пропорциональна скорости циркуляции жидкости; У характеризует разность температур между восходящими и нисходящими потоками жидкости; переменная
Z пропорциональна отклонению вертикального профиля температуры от равновесного значения;
b - безразмерный параметр, определяющий геометрию системы; число Прандтля
σ-физический параметр жидкости, показывающий отношение коэффициентов кинематической вязкости и температуропроводности;
r -управляющий параметр, пропорциональный разности температур, или число Рэлея, нормированное на свое критическое значение.
Система Лоренца в состоянии
 описывать различные этапы эволюции системы: от возникновения конвекции - появления автоколебаний в системе при превышении критического значения температуры, до ее исчезновения при понижении температуры в результате стравливания избытка энергии путем конвекции.
Как известно, конвекция в проводящей среде приводит к генерации магнитного поля посредством механизма гидромагнитного динамо, в результате чего, возможно, и наблюдается 11-летняя цикличность [9]. С другой стороны, были получены указания на то, что фазы солнечного цикла коррелируют с интенсивностью потока солнечных нейтрино. Этот удивительный результат, если он верен, разрушил бы все существующие концепции происхождения солнечного цикла. Это означало бы, что солнечный цикл регулируется процессами, происходящими в глубоких слоях Солнца [10], например, термогравитационной конвекцией Рэлея-Бенара. В рамках предложенной модели природа зарождения 11-летней цикличности не связана с механизмом гидромагнитного динамо.
Описанная выше картина соответствует, очевидно, режиму регулярного аттрактора - области устойчивых траекторий установившихся движений в фазовом пространстве. В этом случае автоколебания носят регулярный характер. Дальнейшее повышение температуры, или увеличение числа Рэлея, играющего роль управляющего параметра, приводит к срыву режима автоколебаний в результате неустойчивости, связанной с неоднозначностью решений при достижении критического значения числа Рэлея.
описывать различные этапы эволюции системы: от возникновения конвекции - появления автоколебаний в системе при превышении критического значения температуры, до ее исчезновения при понижении температуры в результате стравливания избытка энергии путем конвекции.
Как известно, конвекция в проводящей среде приводит к генерации магнитного поля посредством механизма гидромагнитного динамо, в результате чего, возможно, и наблюдается 11-летняя цикличность [9]. С другой стороны, были получены указания на то, что фазы солнечного цикла коррелируют с интенсивностью потока солнечных нейтрино. Этот удивительный результат, если он верен, разрушил бы все существующие концепции происхождения солнечного цикла. Это означало бы, что солнечный цикл регулируется процессами, происходящими в глубоких слоях Солнца [10], например, термогравитационной конвекцией Рэлея-Бенара. В рамках предложенной модели природа зарождения 11-летней цикличности не связана с механизмом гидромагнитного динамо.
Описанная выше картина соответствует, очевидно, режиму регулярного аттрактора - области устойчивых траекторий установившихся движений в фазовом пространстве. В этом случае автоколебания носят регулярный характер. Дальнейшее повышение температуры, или увеличение числа Рэлея, играющего роль управляющего параметра, приводит к срыву режима автоколебаний в результате неустойчивости, связанной с неоднозначностью решений при достижении критического значения числа Рэлея.
НЕОДНОЗНАЧНОСТЬ В ПРИРОДЕ И... НЕ ТОЛЬКО
 С испокон веков нас завораживает вихревое движение ниспадающих потоков водопада, журчание горного ручья, неуловимые сполохи пламени ночного костра. И также вечно одной из нерешенных проблем, стоящих перед естествознанием уже сотни лет, является описание турбулентности.
Многочисленные попытки доказать корректность ряда задач, описываемых уравнениями Навье-Стокса, и, в частности, теоремы существования и единственности в трехмерном случае, предпринимались ведущими математиками в течение десятков лет. Они оказались безрезультатными. Это привело Ж. Лере и других исследователей к мысли, что причина возникших трудностей кроется не в недостатках существующего математического аппарата, а в фундаментальных свойствах самих уравнений Навье-Стокса. Альтернативная гипотеза, связанная с возможной причиной некорректности задачи гидродинамической турбулентности, состоит в том, что решение уравнения Навье-Стокса существует, однако оно не единственно. Другими словами, одни и те же начальные данные могут определять несколько решений [11].
Неоднозначность - не есть досадное исключение из правил, а удивительный механизм совершения Природой качественных скачков! Естественно, что подмеченное естествоиспытателями у Природы своеобразное «ноу-хау» - неоднозначность -
С испокон веков нас завораживает вихревое движение ниспадающих потоков водопада, журчание горного ручья, неуловимые сполохи пламени ночного костра. И также вечно одной из нерешенных проблем, стоящих перед естествознанием уже сотни лет, является описание турбулентности.
Многочисленные попытки доказать корректность ряда задач, описываемых уравнениями Навье-Стокса, и, в частности, теоремы существования и единственности в трехмерном случае, предпринимались ведущими математиками в течение десятков лет. Они оказались безрезультатными. Это привело Ж. Лере и других исследователей к мысли, что причина возникших трудностей кроется не в недостатках существующего математического аппарата, а в фундаментальных свойствах самих уравнений Навье-Стокса. Альтернативная гипотеза, связанная с возможной причиной некорректности задачи гидродинамической турбулентности, состоит в том, что решение уравнения Навье-Стокса существует, однако оно не единственно. Другими словами, одни и те же начальные данные могут определять несколько решений [11].
Неоднозначность - не есть досадное исключение из правил, а удивительный механизм совершения Природой качественных скачков! Естественно, что подмеченное естествоиспытателями у Природы своеобразное «ноу-хау» - неоднозначность -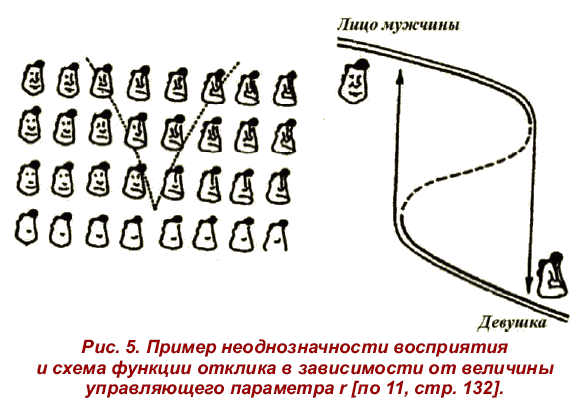 находит свое отражение и в творениях гениальных художников и музыкантов, в частности, в картинах Сальвадора Дали «Невольничий рынок с исчезающим бюстом Вольтера» и Леонардо да Винчи «Джоконда». Не менее интересны в этом плане и удивительные картины-метаморфозы М. К. Эшера (рис. 3).
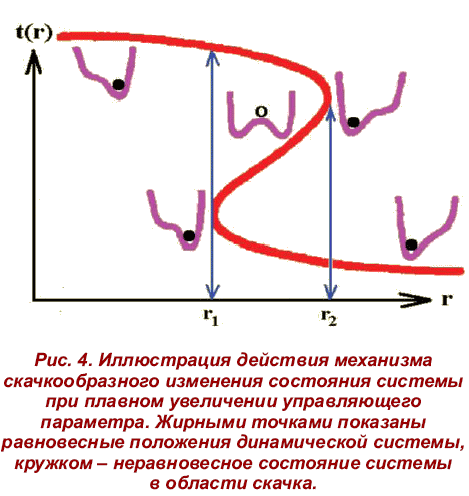
Иллюстрацией действия механизма неоднозначности может служить рис. 4, где 2-образная кривая ((г) представляет собой сечение так называемой «поверхности отклика» динамической системы при непрерывном изменении управляющего параметра г [11]. Зависимость ((г) является неоднозначной функцией переменной г. Для наглядности приводится и характерный вид потенциальной энергии системы при различных значениях управляющего параметра. Устойчивому состоянию соответствует минимум потенциальной энергии (он показан жирной точкой в нижней части кривой потенциала).
Внезапные изменения состояния системы, или «скачки», происходят в точках г, и г2, где внезапно меняется число возможных откликов системы. Рис. 5 достаточно наглядно иллюстрирует подобные скачки в области психологии восприятия (в том числе и известных художественных произведений). Среди представленных фигур четвертая слева в верхнем ряду воспринимается с равной вероятностью как мужское лицо и как фигура девушки. Таким образом, имеем неоднозначность, то есть два возможных отклика при одних и тех же значениях управляющих параметров [11].
находит свое отражение и в творениях гениальных художников и музыкантов, в частности, в картинах Сальвадора Дали «Невольничий рынок с исчезающим бюстом Вольтера» и Леонардо да Винчи «Джоконда». Не менее интересны в этом плане и удивительные картины-метаморфозы М. К. Эшера (рис. 3).
Иллюстрацией действия механизма неоднозначности может служить рис. 4, где 2-образная кривая ((г) представляет собой сечение так называемой «поверхности отклика» динамической системы при непрерывном изменении управляющего параметра г [11]. Зависимость ((г) является неоднозначной функцией переменной г. Для наглядности приводится и характерный вид потенциальной энергии системы при различных значениях управляющего параметра. Устойчивому состоянию соответствует минимум потенциальной энергии (он показан жирной точкой в нижней части кривой потенциала).
Внезапные изменения состояния системы, или «скачки», происходят в точках г, и г2, где внезапно меняется число возможных откликов системы. Рис. 5 достаточно наглядно иллюстрирует подобные скачки в области психологии восприятия (в том числе и известных художественных произведений). Среди представленных фигур четвертая слева в верхнем ряду воспринимается с равной вероятностью как мужское лицо и как фигура девушки. Таким образом, имеем неоднозначность, то есть два возможных отклика при одних и тех же значениях управляющих параметров [11].
МАУНДЕРОВСКИЙ МИНИМУМ - СТРАННЫЙ АТТРАКТОР!
 Срыв автоколебательного режима в системе Лоренца связывается со скачкообразным выходом на странный аттрактор. Наиболее наглядно регулярные и особенно нерегулярные аттракторы можно представить посредством фазовых портретов. Например, колебаниям маятника на фазовой плоскости (в координатах «угол отклонения - скорость маятника») будет соответствовать предельный цикл - регулярный аттрактор.
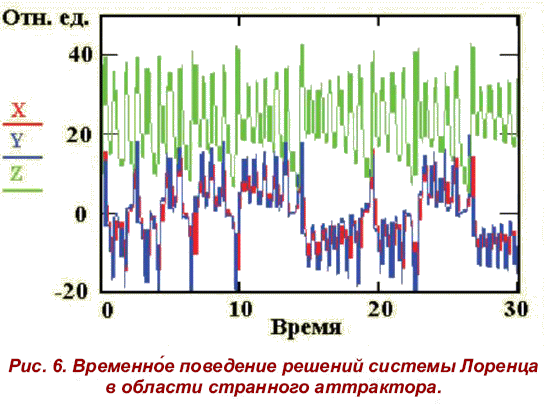
Внезапный срыв автоколебаний (регулярной конвекции) возможен при превышении критического значения числа Рэлея г = 24,74, то есть при выходе системы Лоренца на хаотический, или странный аттрактор (рис. 6,7) [8]. Для сравнения на рис. 7, а показана трехмерная картина фазовой траектории в случае автоколебаний - предельный цикл (г = 17). Разрушению автоколебаний (или предельного цикла) при г = 28 соответствует режим хаотических метаний, или рысканье траектории в трехмерном фазовом объеме в области неоднозначности (рис. 7, б).
Важнейшим свойством хаотического аттрактора Лоренца является его грубость, или структурная устойчивость, которая сохраняется при вариации параметров и начальных условий, так как аттрактор является единственным -
Срыв автоколебательного режима в системе Лоренца связывается со скачкообразным выходом на странный аттрактор. Наиболее наглядно регулярные и особенно нерегулярные аттракторы можно представить посредством фазовых портретов. Например, колебаниям маятника на фазовой плоскости (в координатах «угол отклонения - скорость маятника») будет соответствовать предельный цикл - регулярный аттрактор.
Внезапный срыв автоколебаний (регулярной конвекции) возможен при превышении критического значения числа Рэлея г = 24,74, то есть при выходе системы Лоренца на хаотический, или странный аттрактор (рис. 6,7) [8]. Для сравнения на рис. 7, а показана трехмерная картина фазовой траектории в случае автоколебаний - предельный цикл (г = 17). Разрушению автоколебаний (или предельного цикла) при г = 28 соответствует режим хаотических метаний, или рысканье траектории в трехмерном фазовом объеме в области неоднозначности (рис. 7, б).
Важнейшим свойством хаотического аттрактора Лоренца является его грубость, или структурная устойчивость, которая сохраняется при вариации параметров и начальных условий, так как аттрактор является единственным -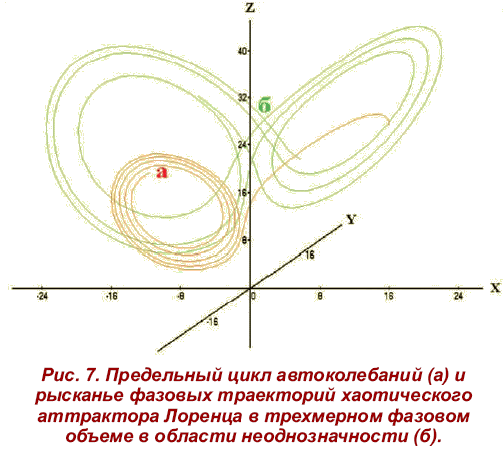 бассейном притяжения служит все фазовое пространство. Таким образом, если уж произошел захват динамической системы (Солнца) в область хаотического аттрактора Лоренца, то это надолго - реализуется очередной маундеровский минимум!? В такой ситуации горизонт предсказуемости ничтожно мал.
Существуют, по меньшей мере, четыре возможных сценария срыва регулярной конвекции (или предельного цикла). Но независимо от сценария, во всех случаях срыва регулярных колебаний в хаотическом спектре появляется так называемая низкочастотная «подложка», или низкочастотный «пьедестал» [13]. Очевидно, это мы и наблюдаем в текущем 23 цикле. Имеется в виду обнаруженный нами дрейф периода солнечной цикличности в низкочастотную область. Важно заметить, что с позиций предлагаемой модели причина подобных сбоев кроется в особенностях самой системы, в данном случае Солнца, а не в каких-либо внешних факторах (приливного воздействия «парада планет», влияния Юпитера и т. д.).
В этой связи следует напомнить, что модель термогравитационной конвекции Рэлея-Бенара, описываемая системой Лоренца (с ее удивительными свойствами) не является частным случаем динамических систем, а есть следствие уравнений движения, выведенных из законов сохранения, вытекающих, в свою очередь, из наблюдаемых свойств пространства-времени, его однородности (во времени и пространстве) и изотропности.
бассейном притяжения служит все фазовое пространство. Таким образом, если уж произошел захват динамической системы (Солнца) в область хаотического аттрактора Лоренца, то это надолго - реализуется очередной маундеровский минимум!? В такой ситуации горизонт предсказуемости ничтожно мал.
Существуют, по меньшей мере, четыре возможных сценария срыва регулярной конвекции (или предельного цикла). Но независимо от сценария, во всех случаях срыва регулярных колебаний в хаотическом спектре появляется так называемая низкочастотная «подложка», или низкочастотный «пьедестал» [13]. Очевидно, это мы и наблюдаем в текущем 23 цикле. Имеется в виду обнаруженный нами дрейф периода солнечной цикличности в низкочастотную область. Важно заметить, что с позиций предлагаемой модели причина подобных сбоев кроется в особенностях самой системы, в данном случае Солнца, а не в каких-либо внешних факторах (приливного воздействия «парада планет», влияния Юпитера и т. д.).
В этой связи следует напомнить, что модель термогравитационной конвекции Рэлея-Бенара, описываемая системой Лоренца (с ее удивительными свойствами) не является частным случаем динамических систем, а есть следствие уравнений движения, выведенных из законов сохранения, вытекающих, в свою очередь, из наблюдаемых свойств пространства-времени, его однородности (во времени и пространстве) и изотропности.
ОЧЕРЕДНОЙ МИФ О ГЛОБАЛЬНОМ ПОТЕПЛЕНИИ?
Сбой 11-летней цикличности может иметь для земной цивилизации далеко идущие последствия. Ослабление солнечной активности будет сопровождаться понижением температуры на Земле, обусловленным, например, механизмом, предложенным академиком РАН Г.Ф. Крымским [14]. Известно, что понижение солнечной активности неизбежно сопровождается повышением интенсивности ГКП. Космические лучи ионизируют воздух на высотах облаков и способствуют образованию там капелек воды. Этим и объясняется тесная связь облачности с космическими лучами. Облачность, в свою очередь, регулирует поступление солнечной энергии на Землю. Эффект понижения средней температуры воздуха в периоды снижения солнечной активности установлен достаточно надежно. Он наиболее выражен в периоды затяжных минимумов солнечной активности. Так, во время минимума Маундера средняя температура воздуха на Земле снизилась на 1 градус [7, 15]. Как уже говорилось выше, увеличение продолжительности солнечного цикла предшествует сбою 11-летней цикличности (минимуму Маундера, в частности) [1]. В таком случае известный эффект глобального потепления за счет антропогенных факторов может оказаться не таким катастрофичным, как это утверждается в средствах массовой информации. Более того, вполне вероятен другой сценарий событий: вместо глобального потепления произойдет глобальное похолодание! А это уже совершенно другая история и в буквальном, и переносном смысле. В случае, если прогнозируемый нами сбой 11-летней цикличности в ближайшее десятилетие подтвердится, то можно будет сделать вывод в пользу солнечной обусловленности не только погоды, но и климата на Земле, причем на интервалах в сотни, тысячи и десятки тысяч лет. Основные положения изложенной выше гипотезы были доложены автором на всероссийской конференции, проходившей в подмосковном г. Троицке в октябре 2005г.(ИЗМИРАН)[16,17].Литература
1. Фрик П.Г. Турбулентность. Подходы и модели. Москва - Ижевск. Институт компьютерных исследований, 2003.-292 с.2. Козлов В.И. Космическая Погода. Мифы и реальность //Наука и техника в Якутии. - № 1 (2). - 2002. -С. 17-20.
3. Козлов В.И. Горизонты предсказуемости. Очевидное - Невероятное // Наука и техника в Якутии. -№2(5).-2002.-С. 11-14.
4. Kozlov V.I., Kozlov V.V., Markov V.V. Effect of polaririty reversal of solar magnetic field in cosmic ray fluctuations// Proceeding on ISCS-2003 simposium "Solar variaability as an input to the Earth`s enviroment". Taranska Lomnica. Slovakia. 23-28 June,2003 -P.117-120.
5. Витинский Ю.И., Копецкий М., Куклин Г.В. Статистика пятнообразовательной деятельности Солнца. - Москва: Наука, 1986. -201с.
6. Кононович Э.В. Аналитические представления средних вариаций солнечной активности в течение цикла // Геомагнетизм и аэрономия. - 2005. - Т. 45.-№3.-С. 316-323.
7. Комитов Б.П., Кафтан В.И. Изменения солнечной активности последних тысячелетий. Возможен ли очередной долгопериодический солнечный минимум? // Геомагнетизм и аэрономия. - 2003. - Т. 43. - № 5. -С. 592-601.
8. Морозов А.Д., Драгунов Т.Н. Визуализация и анализ инвариантных множеств динамических систем. -М.: Институт компьютерных исследований, 2003. -304 с.
9. Зельдович Я.Б., Рузмайкин А.А. Гидромагнитное динамо как источник планетарного, солнечного и галактического магнетизма // Успехи физических наук. - 1987. -Т. 152.- Вып. 2. - С. 263-284.
10. Долгинов А.З. О происхождении магнитных полей Земли и небесных тел // Успехи физических наук. - 1987. -Т. 152.- Вып. 2. - С. 231-262.
11. Малинецкий Г.Г. Математические основы синергетики. Хаос, структуры, вычислительный эксперимент. - Москва: Эдиториал УРСС, 2000. - 256 с.
12. http://www.esher.ru/index.php
13. Данилов Ю.А. Лекции по нелинейной динамике. -Москва: Постмаркет, 2001. -192 с.
14. Крымский Г.Ф. Космические лучи и погода // Наука и техника в Якутии.-№ 1(8).-2005.-С. 3-6.
15. http://www.polotsk.nm.ru/nep1.htm
16. Козлов В.И., Марков В.В. Вейвлет-образ волны переполюсовки общего магнитного поля Солнца по исследованию флуктуации космических лучей за циклы ХХ-ХХШ // Геомагнетизм и аэрономия. - 2006 (в печати).
17. http://www.forshock.ru